Расчет Объема Цилиндрической Емкости
Ага, сегодня я путем несложных умозаключений буду выяснять объем жидкости, находящейся в цилиндрической таре, лежащей на боку. И это не праздности ради, а дела. Цитирую запрос пользователя: Доброго времени суток. Видел калькулятор объема сегмента цилиндра, но нужно немножко другое. По работе приходится измерять количество жидкости в таре. Так вот допустим тара цилиндрической формы R=1,13м и H=6,3м лежит на поверхности.
Apr 3, 2012 - Определение объема жидкости в цилиндрическом горизонтальном резервуаре измерением глубины жидкости. Подарок королевам бензоколонок. Тем, кто измеряет горючку очень длинной линейкой посвящается. Как-то попросила знакомая заправщица автоматизировать расчёт столь. Расчет объема. Объем горизонтально лежащей овальной или цилиндрической емкости.
Жидкости в таре 0,9м от поверхности. Вопрос: какой объем жидкости в таре? Там дальше в запросе идут ссылки на решение, но это же не спортивно, поэтому я пошел своим путем:) Сразу замечу, что вторая, более сложная задача — объем жидкости в таре, лежащей под наклоном, еще ждет своего решения. Банковский бизнес. Вот калькулятор, который все считает, а ход рассуждений, как обычно, под ним. Итак, сформулируем задачу наглядно, и посмотрим на цилиндр в разрезе (см. Если уровень жидкости m больше половины, то находим объем воздуха в оставшейся части, а потом вычитаем из общего объема — т. е. Всегда сводим к случаю, изображенному на рисунке.
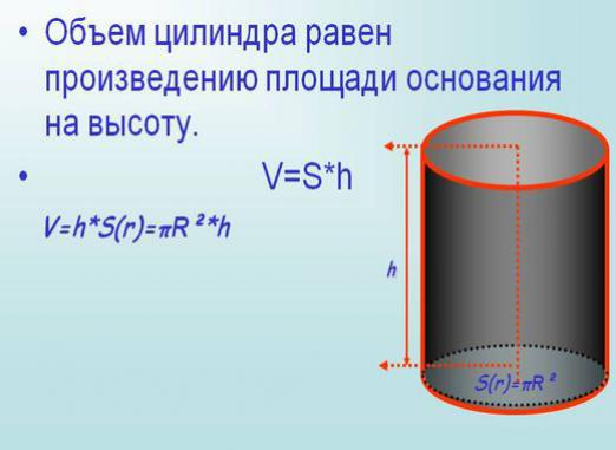
Формула объема всего цилиндра известна — площадь основания, помноженная на высоту. А нам, значит, надо найти площадь фигуры, залитой синей жидкостью, и тоже помножить на высоту. Пытливый взгляд отметит, что фигура, залитая синей жидкостью, получается из сектора после вычета верхнего треугольника. Площадь сектора находится как, где альфа — это угол дуги в радианах. Угол дуги нам неизвестен.
Разберемся сначала с ним. Линия, опущенная вертикально вниз делит верхний треугольник на два прямоугольных треугольника.
Расчет Объема Цилиндрической Емкости Калькулятор
Гипотенуза у них равна R, а катет, прилежащий к верхнему углу, равен R-m. Таким образом, соответственно и ответ нам Javascript даст как раз в радианах, то что нам нужно. Теперь разберемся с верхним треугольником. Он равнобедренный, бедра равны R, а основание нам неизвестно. А оно как раз равно удвоенному противолежащему катету, который, согласно всем известной теореме Пифагора равен Зная все стороны треугольника, нетрудно найти его площадь по формуле Герона —. Где Вот, собственно, и все. Мы знаем площадь сектора и площадь треугольника.
Вычитаем площадь треугольника из площади сектора, домножаем на высоту цилиндра (или длину цилиндра, с учетом того, что он лежит) и получаем результат.
Подарок королевам бензоколонок. Тем, кто измеряет горючку очень длинной линейкой посвящается. Как-то попросила знакомая заправщица автоматизировать расчёт столь важной для неё процедуры, и оказалось не всё так просто как на первый взгляд кажется.
Программно или с помощью Windows Shell Scrap Object Handler (shscrap.dll) — двойным щелчком мыши или из командной строки Windows Таким образом, перед тем как просмотреть внутренности shs, убедитесь каспером, доктор вебом, пандой или хоть чем, что вируса внутри нет. А оно нам надо? Программный способ открытия shs Этот способ лучше подходит, если времени мало и разбираться куда и как засовывать dll нет особого желания, а shs уже тут и просит открытия. Как открыть расширение tst. Так как сам файл содержит фрагменты, куски чего-то пока нам непонятного и обязательно исполняемого, вероятность того, что внутри вирус — довольно велика.
Данным вопросом до меня занимался Государственный научный метрологический центр - Всероссийский научно-исследовательский институт расходометрии (ГНМЦ - ВНИИР) Госстандарта России. В итоге разработал, а Межгосударственный Совет по стандартизации, метрологии и сертификации (протокол № 17 от 22 июня 2000 г.) принял ГОСТ 8.346-2000 ' РЕЗЕРВУАРЫ СТАЛЬНЫЕ ГОРИЗОНТАЛЬНЫЕ ЦИЛИНДРИЧЕСКИЕ'. Охренительный труд. В общем, пришлось помочь даме в преддверие 8 марта.
Может кому поможет ещё. Вот полученная мной секретная формула: 'Объём: '+Окр((R.R.(PI-arccos((h-R)/R)) + (h-R).sqrt(2.R.h-h.h)).L.1000,0)+' л' В обработке использовал пару функций VBscript. Ну, это ОЧЕНЬ частный случай. Я несколько лет работал на заправке.
И вот что скажу: 1) очень редко резервуар лежит (стоит) строго горизонтально 2) очень редко резервуар имеет строго цилиндрическую формую. Как правило, есть крышки (донца) либо конической, либо сферической формы. И не факт, что они приварены строго по оси 3) внутри резервуара есть ребра жесткости, имеющие относительно приличный объем. И поскольку учет на заправках (как правило) ведется с точностью до литра, то такая метода учета не может быть рекомендована для этой цели. Единственные резервуары, сделанные строго по размерам - это ЖД цистерны.
И то, для них существуют типовые таблицы, а не формулы пересчета. А еще был у меня такой резервуар, который то ли качался под землей на какой-то опоре, то ли 'хлопал' под нагрузкой. В определенном диапазоне происходил скачек показаний, который нельзя было никак уловить. Дважды его тарировали, но так и не вычислили этот момент.
Расчет Объема Топлива В Цилиндрической Емкости
Сделайте даме еще приятней. У нее есть тарировочные таблицы. Выглядят так- высота взлива (мм)= вместимость, коэфт уточнения, погрешность. Делаем 1-й справочник - емкость, ему подчиненный тарировочная таблица с реквизитами и обработочка с проходом по тарировочной таблице. Действительно формулой вы ее подставляете тк емкости при заполнении как правило 'гуляют'. Здесь согласен с 4.
Но и жд цистерны тоже несовсем точны из-за того что делают их люди и на таких размерах трудно уловить литр. Для примера 1см на высоте 2м цистерны типа 62 дает прирост топлива 300 литров, да плюс шток можно чуток приударить или чуток невертикально поставить, пол см. Спокойно набегает. А по деньгам - это уже хорошо. Лучше уж сделайте эти два справочника.